葛瑞斯肯樂活筆記

假設我們擁有一串數字: 5,12,33,19,40,41, 這些數字均各自代表每個字串從文本取得的頻率資訊。

舉例來說，我(5), 想要(12), 車站(33), 汽車(19), 車牌(40), 轉彎(41)。

•在建構 Huffman tree (霍夫曼樹)前，我們要先針對此數字串進行小到大的排序，會得到下列的結果:

•5,12,19,33,40,41

•接下來我們開始介紹如何建構  Huffman tree (霍夫曼樹):

節點結合步驟: 每次都挑兩個最小值的節點進行合併

合併會產生一個新節點，並且依大小排入尚未合併的數字串中

移動33與36

移動40與41

最後合併成一棵樹為止

接著節點的左邊為0，右邊為1

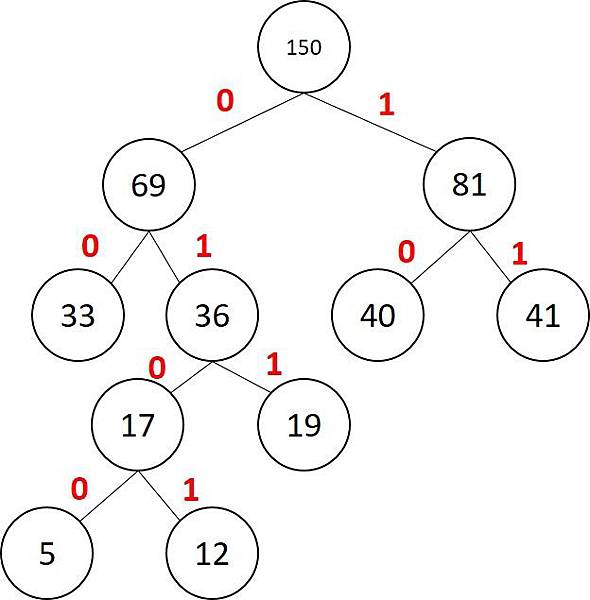
然後我們針對葉節點(原本的數字)進行編碼，從最高層的葉節點開始編碼。

然後從第二層的葉節點開始編碼。

然後從第三層的葉節點開始編碼。

資料壓縮率

轉換回原來對應的文本概念，就是每個數字代表字串出現在文本的頻率:

•原本的資料量: 8 bit*(5+12+19+33+40+41) = 1200 (假設一開始的每個詞彙均為 8bit)

•霍夫曼編碼後: 2*(33+40+41)+3*(19)+4*(5+12) = 353

•壓縮率 = (1- (353/1200))*100%, = 70.58%